この記事はレイトレアドベントカレンダー2021 24日目の記事です。この記事ではモンテカルロレイトレーシングを用いた一様媒質のボリュームレンダリングの理論的な部分について解説しています。
ボリュームレンダリング方程式をモンテカルロ積分する
指数分布を用いて自由行程サンプリングを行う
ロシアンルーレットによって吸収/散乱イベントの選択を行う
位相関数を用いて散乱方向のサンプリングを行う
一様媒質(Homogeneous Medium) とは媒質中で吸収係数(Absorption Coefficient) /散乱係数(Scattering coefficient) が一定となっている媒質のことを言います。水や空気などは一様媒質に近い媒質です。レンダリングでは人間の皮膚もよく一様媒質としてモデル化されます。
媒質中では光は吸収/散乱を繰り返します。それぞれの強さは吸収係数/散乱係数で制御されます。吸収を強くすると媒質の見た目は暗くなり、散乱を強くすると光がボヤけて柔らかい印象が得られるようになります。
以下の画像は一様媒質のレンダリングの例です。手前側が一様媒質でモデル化された物体、奥側が媒質を考慮せずに、表面だけLambert BRDFでモデル化した物体です。
一様媒質のレンダリングの例 一様媒質を考慮した物体では光が滲んで柔らかい印象になっていることが分かると思います。これは媒質中で光が散乱を繰り返して拡散するためです。
特に、物体の後ろ側に光源がある場合は一様媒質のモデルでは光が媒質中を透過するため、物体の厚さが薄い箇所では光が透けて見えます。一方で媒質を考慮していない物体では光は全く透過しません。
光が透過する例 これらは 表面化散乱(Subsurface scattering) の例になっています。
このような質感を表現するためには ダイポールモデル (Dipole model)Random walk subsurface scattering と言われたりします。
媒質中ではレイがランダムに動き続ける モンテカルロレイトレーシングによる一様媒質のレンダリングでは、媒質の中を散乱によってレイがランダムに動き続けます。Random walk subsurface scatteringという名前がついているのはこの様子がRandom walkに見えるからだと思います。
近似モデルは高速にレンダリングが可能ですが、あくまで近似なので見た目は不正確になる場合があります。一方でモンテカルロレイトレーシングによる方法では計算量は多くなりますが、正確な見た目を表現することが出来ます。
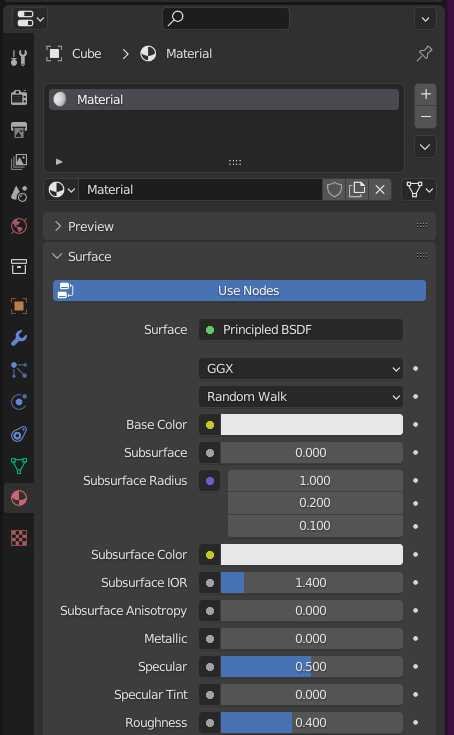
BlenderのPrincipled BSDFにもSubsurfaceの選択欄でRandom walkという項目があり、これを選択すれば表面化散乱がモンテカルロレイトレーシングで計算されるようになっています。
BlenderのPrincipled BSDF こういった表面化散乱以外にも、水や霧のレンダリングに一様媒質を用いることが出来ます。以下はコーネルボックスに霧を充満させてレンダリングした例です。
霧が充満したコーネルボックス 光源の周りが霧による光の散乱によってボヤけた感じになっていることが分かります。
このように一様媒質を考慮したレンダリングを行うとレンダリングの表現力が一気に上がります。
以降ではモンテカルロレイトレーシングを用いて一様媒質のレンダリングを行う方法について見ていきます。
まずは何を計算すれば良いのかをはっきりさせます。そのために媒質中での放射輝度の変化を記述するRTEとVREという式について見ていきます。
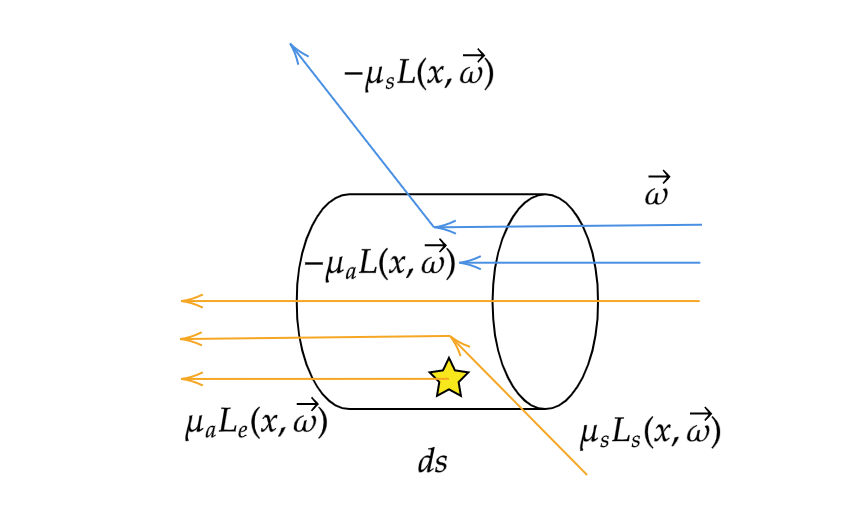
媒質中での放射輝度の変化は以下の 放射輸送方程式(Radiative transfer equation - RTE) によって記述されます。
L ( x , ω ⃗ ) L(x, \vec{\omega}) L ( x , ω ) x x x ω ⃗ \vec{\omega} ω μ a ( x ) \mu_a(x) μ a ( x ) x x x μ s ( x ) \mu_s(x) μ s ( x ) x x x L e ( x , ω ⃗ ) L_e(x, \vec{\omega}) L e ( x , ω ) x x x ω ⃗ \vec{\omega} ω L s ( x , ω ⃗ ) L_s(x, \vec{\omega}) L s ( x , ω ) x x x ω ⃗ \vec{\omega} ω
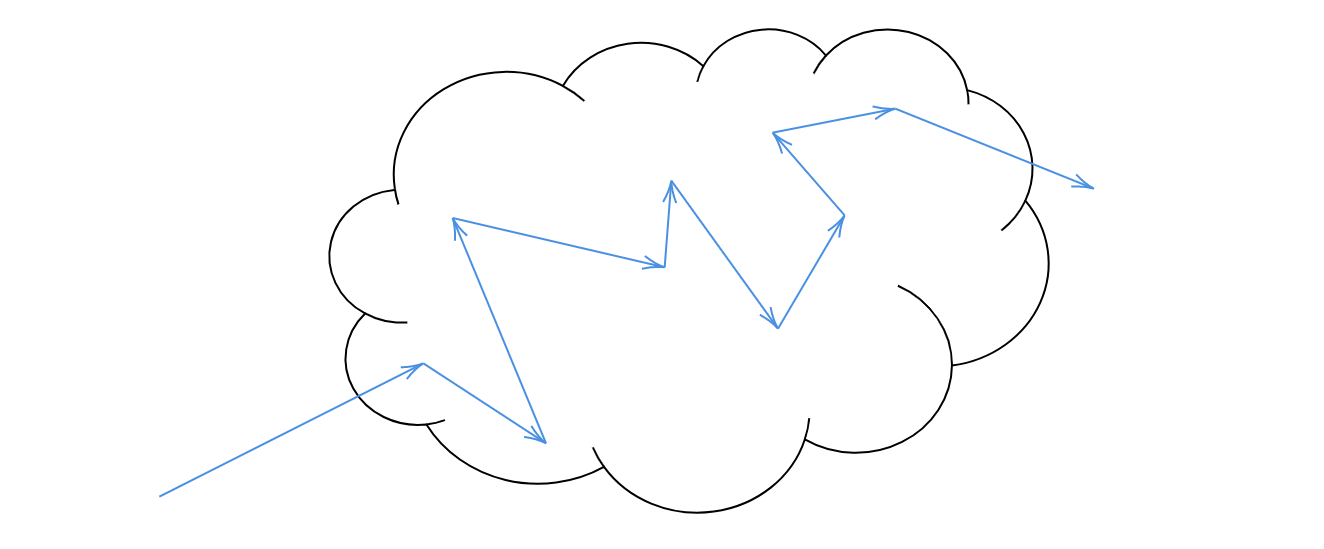
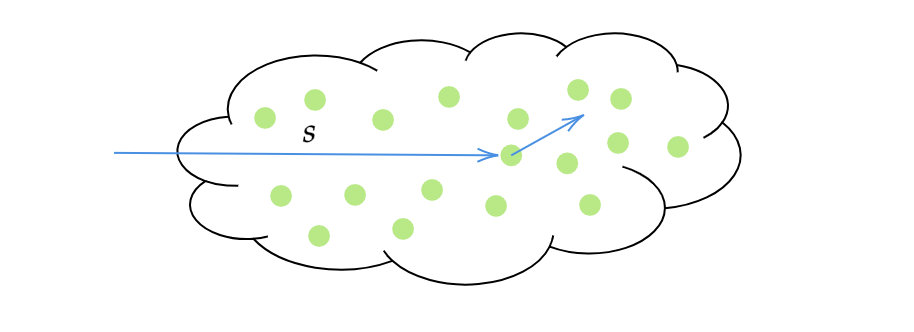
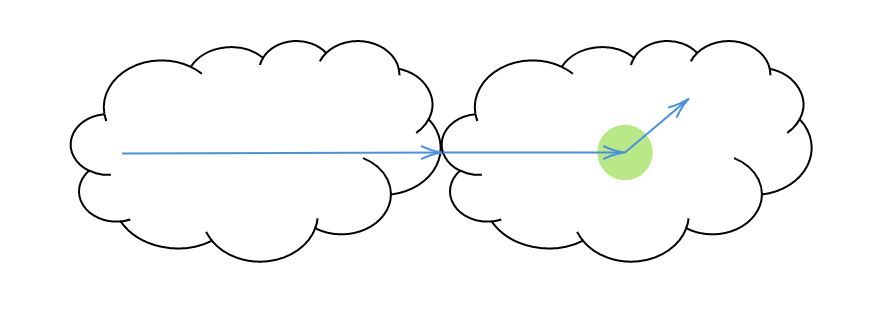
( ω ⃗ ⋅ ∇ ) L ( x , ω ⃗ ) = − μ a ( x ) L ( x , ω ⃗ ) − μ s ( x ) L ( x , ω ⃗ ) + μ a ( x ) L e ( x , ω ⃗ ) + μ s ( x ) L s ( x , ω ⃗ ) (1) (\vec{\omega}\cdot \nabla)L(x, \vec{\omega}) = -\mu_a(x)L(x, \vec{\omega}) - \mu_s(x)L(x,\vec{\omega}) + \mu_a(x)L_e(x, \vec{\omega}) + \mu_s(x)L_s(x, \vec{\omega}) \tag{1} ( ω ⋅ ∇ ) L ( x , ω ) = − μ a ( x ) L ( x , ω ) − μ s ( x ) L ( x , ω ) + μ a ( x ) L e ( x , ω ) + μ s ( x ) L s ( x , ω ) ( 1 ) 式(1)の概念図 この方程式は方向ω ⃗ \vec{\omega} ω d s ds d s
− μ a ( x ) L ( x , ω ⃗ ) -\mu_a(x)L(x, \vec{\omega}) − μ a ( x ) L ( x , ω ) − μ s ( x ) L ( x , ω ⃗ ) -\mu_s(x)L(x, \vec{\omega}) − μ s ( x ) L ( x , ω ) μ a ( x ) L e ( x , ω ⃗ ) \mu_a(x)L_e(x, \vec{\omega}) μ a ( x ) L e ( x , ω ) μ s ( x ) L s ( x , ω ⃗ ) \mu_s(x)L_s(x, \vec{\omega}) μ s ( x ) L s ( x , ω )
吸収係数/散乱係数は本来は波長依存の量ですが、今回は簡単のために波長非依存の量であると仮定して話を進めます。
ここでL s ( x , ω ⃗ ) L_s(x, \vec{\omega}) L s ( x , ω )
S 2 \mathcal{S^2} S 2 f p ( ω ⃗ , ω ⃗ ′ ) f_p(\vec{\omega}, \vec{\omega}') f p ( ω , ω ′ ) L i ( x , ω ⃗ ′ ) L_i(x, \vec{\omega}') L i ( x , ω ′ ) x x x ω ⃗ ′ \vec{\omega}' ω ′
L s ( x , ω ⃗ ) = ∫ S 2 f p ( ω ⃗ , ω ⃗ ′ ) L i ( x , ω ⃗ ′ ) d σ ( ω ⃗ ′ ) (2) L_s(x, \vec{\omega}) = \int_{\mathcal{S}^2} f_p(\vec{\omega}, \vec{\omega}')L_i(x, \vec{\omega}')d\sigma(\vec{\omega}') \tag{2} L s ( x , ω ) = ∫ S 2 f p ( ω , ω ′ ) L i ( x , ω ′ ) d σ ( ω ′ ) ( 2 ) 式(2)の概念図 この式は媒質中で周辺から入ってきた光が方向ω ⃗ \vec{\omega} ω f p f_p f p
式(1)はL s L_s L s (Integro-differential equation) になっています。このままでは扱いづらいので、両辺を積分して微分を消すことを考えます。
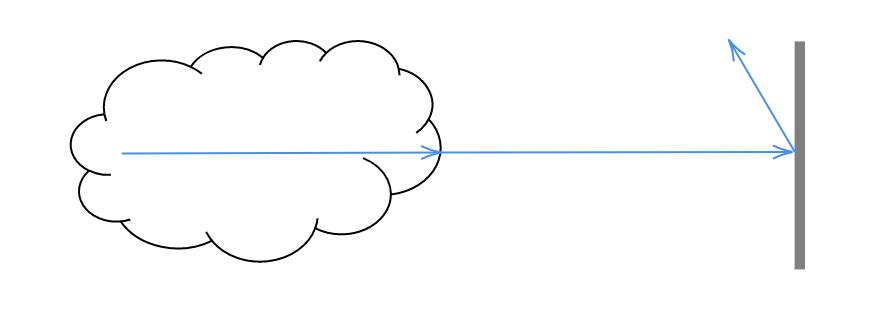
境界条件として点x x x t t t x − t ω ⃗ x - t\vec{\omega} x − t ω 0 0 0 t t t
μ t ( x ) = μ a ( x ) + μ s ( x ) \mu_t(x) = \mu_a(x) + \mu_s(x) μ t ( x ) = μ a ( x ) + μ s ( x ) T ( x , x − s ω ⃗ ) = e − ∫ 0 s μ t ( x − s ′ ω ⃗ ) d s ′ T(x, x - s\vec{\omega}) = e^{-\int_0^s \mu_t(x - s'\vec{\omega})ds'} T ( x , x − s ω ) = e − ∫ 0 s μ t ( x − s ′ ω ) d s ′
L ( x , ω ⃗ ) = ∫ 0 t T ( x , x − s ω ⃗ ) ( μ a ( x − s ω ⃗ ) L e ( x − s ω ⃗ , ω ⃗ ) + μ s ( x − s ω ⃗ ) L s ( x − s ω ⃗ , ω ⃗ ) ) d s + T ( x , x − t ω ⃗ ) L ( x − t ω ⃗ , ω ⃗ ) (3) \begin{aligned}
L(x, \vec{\omega}) &= \int_0^t T(x, x - s\vec{\omega})\bigg( \mu_a(x - s\vec{\omega})L_e(x - s\vec{\omega}, \vec{\omega}) + \mu_s(x - s\vec{\omega})L_s(x - s\vec{\omega}, \vec{\omega}) \bigg)ds \\
&+ T(x, x - t\vec{\omega})L(x - t\vec{\omega}, \vec{\omega}) \tag{3}
\end{aligned} L ( x , ω ) = ∫ 0 t T ( x , x − s ω ) ( μ a ( x − s ω ) L e ( x − s ω , ω ) + μ s ( x − s ω ) L s ( x − s ω , ω ) ) d s + T ( x , x − t ω ) L ( x − t ω , ω ) ( 3 ) 式(3)の概念図 この式は ボリュームレンダリング方程式(Volume rendering equation - VRE) と呼ばれます。レンダリング方程式のボリューム版です。
第1項の積分は媒質中から得られる放射輝度の合計を表しています。第2項は媒質の終端から入射する放射輝度を表しています。
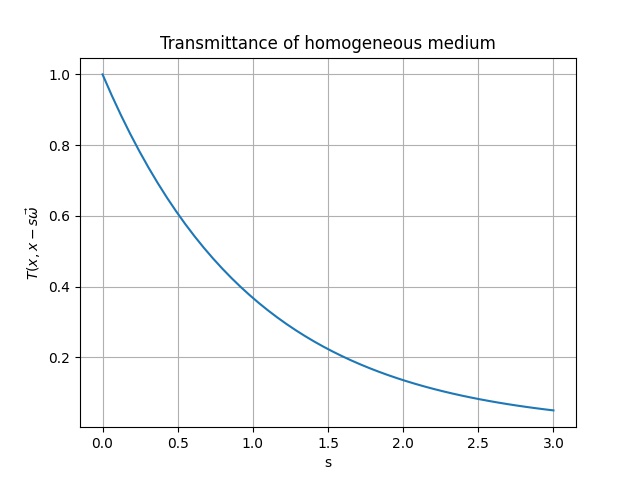
T ( x , x − s ω ⃗ ) T(x, x - s\vec{\omega}) T ( x , x − s ω ) 透過率(Transmittance) と呼ばれます。この関数は光が点x − s ω ⃗ x - s\vec{\omega} x − s ω x x x μ t ( x ) \mu_t(x) μ t ( x ) 消失係数(Extinction coefficient) と言います。
式(3)はL s L_s L s L i ( x , ω ⃗ ′ ) L_i(x, \vec{\omega}') L i ( x , ω ′ )
ボリュームレンダリングでは式(3)のボリュームレンダリング方程式を数値計算することが目標になります 。
モンテカルロレイトレーシングによるボリュームレンダリングでは式(3)をモンテカルロ積分します。以降ではその方法について見ていきます。
第1項の積分では積分変数として距離s s s
距離s s s S : Ω → [ 0 , ∞ ) S: \Omega \to [0, \infty) S : Ω → [ 0 , ∞ ) Ω \Omega Ω S S S [ 0 , ∞ ) [0, \infty) [ 0 , ∞ ) S ≥ t S \ge t S ≥ t S S S ロシアンルーレット によって第1項と第2項のどちらを評価するかを確率的に選択します。
この時、式(3)のモンテカルロ積分は以下のように書けます。
p S ( s ) p_S(s) p S ( s ) S S S 1 A \mathbb{1}_A 1 A A A A P ( S ≥ t ) P(S \ge t) P ( S ≥ t ) S S S t t t
T e r m 1 ( s ) = T ( x , x − s ω ⃗ ) ( μ a ( x − s ω ⃗ ) L e ( x − s ω ⃗ , ω ⃗ ) + μ s ( x − s ω ⃗ ) L s ( x − s ω ⃗ , ω ⃗ ) ) T e r m 2 = T ( x , x − t ω ⃗ ) L ( x − t ω ⃗ , ω ⃗ ) L ^ ( x , ω ⃗ ) = T e r m 1 ( s ) p S ( s ) 1 { s < t } + T e r m 2 P ( S ≥ t ) 1 { s ≥ t } (4) \begin{aligned}
\mathrm{Term1}(s) &= T(x, x - s\vec{\omega})\bigg( \mu_a(x - s\vec{\omega})L_e(x - s\vec{\omega}, \vec{\omega}) + \mu_s(x - s\vec{\omega})L_s(x - s\vec{\omega}, \vec{\omega}) \bigg) \\
\mathrm{Term2} &= T(x, x - t\vec{\omega})L(x - t\vec{\omega}, \vec{\omega}) \\
\widehat{L}(x, \vec{\omega}) &= \frac{\mathrm{Term1}(s)}{p_S(s)}\mathbb{1}_{\{s < t\}} + \frac{\mathrm{Term2}}{P(S \ge t)}\mathbb{1}_{\{s \ge t\}} \tag{4}
\end{aligned} T e r m 1 ( s ) T e r m 2 L ( x , ω ) = T ( x , x − s ω ) ( μ a ( x − s ω ) L e ( x − s ω , ω ) + μ s ( x − s ω ) L s ( x − s ω , ω ) ) = T ( x , x − t ω ) L ( x − t ω , ω ) = p S ( s ) T e r m 1 ( s ) 1 { s < t } + P ( S ≥ t ) T e r m 2 1 { s ≥ t } ( 4 ) これが式(3)の不偏推定量になっていることは以下のように確認できます。
E [ L ^ ( x , ω ⃗ ) ] = ∫ 0 ∞ ( T e r m 1 ( s ) p S ( s ) 1 { s < t } + T e r m 2 P ( S ≥ t ) 1 { s ≥ t } ) p S ( s ) d s = ∫ 0 ∞ T e r m 1 ( s ) p S ( s ) 1 { s < t } p S ( s ) d s + T e r m 2 P ( S ≥ t ) ∫ 0 ∞ 1 { s ≥ t } p S ( s ) d s = ∫ 0 t T e r m 1 ( s ) p S ( s ) p S ( s ) d s + T e r m 2 P ( S ≥ t ) P ( S ≥ t ) = ∫ 0 t T e r m 1 ( s ) d s + T e r m 2 \begin{aligned}
\mathbb{E}[\widehat{L}(x, \vec{\omega})] &= \int_0^{\infty}\bigg(\frac{\mathrm{Term1}(s)}{p_S(s)}\mathbb{1}_{\{s < t\}} + \frac{\mathrm{Term2}}{P(S \ge t)}\mathbb{1}_{\{s \ge t\}}\bigg)p_S(s)ds \\
&= \int_0^{\infty}\frac{\mathrm{Term1}(s)}{p_S(s)}\mathbb{1}_{\{s < t\}}p_S(s)ds + \frac{\mathrm{Term2}}{P(S \ge t)}\int_0^{\infty}\mathbb{1}_{\{s \ge t\}}p_S(s)ds \\
&= \int_0^t\frac{\mathrm{Term1}(s)}{p_S(s)}p_S(s)ds + \frac{\mathrm{Term2}}{P(S \ge t)}P(S \ge t) \\
&= \int_0^t \mathrm{Term1}(s)ds + \mathrm{Term2}
\end{aligned} E [ L ( x , ω ) ] = ∫ 0 ∞ ( p S ( s ) T e r m 1 ( s ) 1 { s < t } + P ( S ≥ t ) T e r m 2 1 { s ≥ t } ) p S ( s ) d s = ∫ 0 ∞ p S ( s ) T e r m 1 ( s ) 1 { s < t } p S ( s ) d s + P ( S ≥ t ) T e r m 2 ∫ 0 ∞ 1 { s ≥ t } p S ( s ) d s = ∫ 0 t p S ( s ) T e r m 1 ( s ) p S ( s ) d s + P ( S ≥ t ) T e r m 2 P ( S ≥ t ) = ∫ 0 t T e r m 1 ( s ) d s + T e r m 2 距離サンプリングを用いた式(4)の計算の物理的意味について考えてみると、距離s s s s s s s s s 自由行程サンプリング(Free-path sampling) と呼ばれます。
自由行程サンプリング 続いてS S S
S S S 式(4)を見ると、透過率T T T S S S T T T 重点的サンプリング が行えるので、そのようにします。
S S S p S ( s ) p_S(s) p S ( s ) k k k S S S
p S ( s ) = k T ( x , x − s ω ⃗ ) p_S(s) = kT(x, x - s\vec{\omega}) p S ( s ) = k T ( x , x − s ω ) これが確率密度関数になるためには∫ 0 ∞ p S ( s ) d s = 1 \int_0^{\infty} p_S(s)ds = 1 ∫ 0 ∞ p S ( s ) d s = 1 k k k
今考えているのは一様媒質なので、μ t ( x ) \mu_t(x) μ t ( x ) 透過率T T T 。
T ( x , x − s ω ⃗ ) = e − ∫ 0 s μ t ( x − s ′ ω ⃗ ) d s ′ = e − ∫ 0 s μ t d s ′ = e − μ t s (5) \begin{aligned}
T(x, x - s\vec{\omega}) &= e^{-\int_0^s \mu_t(x - s'\vec{\omega})ds'} \\
&= e^{-\int_0^s \mu_t ds'} \\
&= e^{-\mu_t s} \tag{5}
\end{aligned} T ( x , x − s ω ) = e − ∫ 0 s μ t ( x − s ′ ω ) d s ′ = e − ∫ 0 s μ t d s ′ = e − μ t s ( 5 ) 一様媒質の場合の透過率 式(5)を使って∫ 0 ∞ p S ( s ) d s \int_0^{\infty} p_S(s)ds ∫ 0 ∞ p S ( s ) d s
∫ 0 ∞ p S ( s ) d s = k ∫ 0 ∞ T ( x , x − s ω ⃗ ) d s = k 1 μ t \begin{aligned}
\int_0^{\infty} p_S(s)ds &= k\int_0^{\infty} T(x, x - s\vec{\omega})ds \\
&= k\frac{1}{\mu_t}
\end{aligned} ∫ 0 ∞ p S ( s ) d s = k ∫ 0 ∞ T ( x , x − s ω ) d s = k μ t 1 これが1になれば良いので、k = μ t k = \mu_t k = μ t S S S
p S ( s ) = μ t T ( x , x − s ω ⃗ ) = μ t e − μ t s (6) \begin{aligned}
p_S(s) &= \mu_t T(x, x - s\vec{\omega}) \\
&= \mu_t e^{-\mu_t s} \tag{6}
\end{aligned} p S ( s ) = μ t T ( x , x − s ω ) = μ t e − μ t s ( 6 ) これは指数分布 の確率密度関数と同じです。つまりS S S 1 μ t \frac{1}{\mu_t} μ t 1
これでS S S
S S S 今回の場合S S S 逆関数法 を用いてS S S
S S S F S ( s ) F_S(s) F S ( s )
F S ( s ) = ∫ 0 s p S ( s ) d s = 1 − e − μ t s (7) \begin{aligned}
F_S(s) &= \int_0^s p_S(s)ds \\
&= 1 - e^{-\mu_t s} \tag{7}
\end{aligned} F S ( s ) = ∫ 0 s p S ( s ) d s = 1 − e − μ t s ( 7 ) 累積分布関数の逆関数を求めると以下のようになります。
F S − 1 ( u ) = − log ( 1 − u ) μ t F_S^{-1}(u) = -\frac{\log(1 - u)}{\mu_t} F S − 1 ( u ) = − μ t log ( 1 − u ) [ 0 , 1 ] [0, 1] [ 0 , 1 ] ξ \xi ξ F S − 1 ( ξ ) F_S^{-1}(\xi) F S − 1 ( ξ ) S S S s s s
s = − log ( 1 − ξ ) μ t (8) s = -\frac{\log(1 - \xi)}{\mu_t} \tag{8} s = − μ t log ( 1 − ξ ) ( 8 ) これで重点的サンプリングを用いて距離S S S s s s
sのヒストグラム 大体指数分布に従っている様子が分かります。
次は式(4)の各項の評価方法について見ていきます。
T e r m 1 \mathrm{Term1} T e r m 1 T e r m 1 \mathrm{Term1} T e r m 1
T e r m 1 ( s ) = T ( x , x − s ω ⃗ ) ( μ a ( x − s ω ⃗ ) L e ( x − s ω ⃗ , ω ⃗ ) + μ s ( x − s ω ⃗ ) L s ( x − s ω ⃗ , ω ⃗ ) ) \mathrm{Term1}(s) = T(x, x - s\vec{\omega})\bigg( \mu_a(x - s\vec{\omega})L_e(x - s\vec{\omega}, \vec{\omega}) + \mu_s(x - s\vec{\omega})L_s(x - s\vec{\omega}, \vec{\omega}) \bigg) T e r m 1 ( s ) = T ( x , x − s ω ) ( μ a ( x − s ω ) L e ( x − s ω , ω ) + μ s ( x − s ω ) L s ( x − s ω , ω ) ) 今考えているのは一様媒質なので、μ a \mu_a μ a μ s \mu_s μ s
T e r m 1 ( s ) = T ( x , x − s ω ⃗ ) ( μ a L e ( x − s ω ⃗ , ω ⃗ ) + μ s L s ( x − s ω ⃗ , ω ⃗ ) ) \mathrm{Term1}(s) = T(x, x - s\vec{\omega})\bigg( \mu_a L_e(x - s\vec{\omega}, \vec{\omega}) + \mu_s L_s(x - s\vec{\omega}, \vec{\omega}) \bigg) T e r m 1 ( s ) = T ( x , x − s ω ) ( μ a L e ( x − s ω , ω ) + μ s L s ( x − s ω , ω ) ) 今、距離S S S s s s T T T
T ( x , x − s ω ⃗ ) = e − μ t t T(x, x - s\vec{\omega}) = e^{-\mu_t t} T ( x , x − s ω ) = e − μ t t 問題はL e L_e L e L s L_s L s L s L_s L s L e L_e L e L s L_s L s 吸収/散乱イベントサンプリング と呼ぶことにします。吸収イベントが選択されたらL e L_e L e L s L_s L s
吸収イベントを選択する確率をP a P_a P a P s = 1 − P a P_s = 1 - P_a P s = 1 − P a [ 0 , 1 ] [0, 1] [ 0 , 1 ] ξ \xi ξ T e r m 1 \mathrm{Term1} T e r m 1
T e r m 1 ^ ( s ) = T ( x , x − s ω ⃗ ) ( μ a L e ( x − s ω ⃗ , ω ⃗ ) P a 1 { ξ < P a } + μ s L s ( x − s ω ⃗ , ω ⃗ ) P s 1 { ξ ≥ P a } ) (9) \widehat{\mathrm{Term1}}(s) = T(x, x - s\vec{\omega})\bigg( \frac{\mu_a L_e(x - s\vec{\omega}, \vec{\omega})}{P_a}\mathbb{1}_{\{\xi < P_a\}} + \frac{\mu_s L_s(x - s\vec{\omega}, \vec{\omega})}{P_s}\mathbb{1}_{\{\xi \ge P_a\}} \bigg) \tag{9} T e r m 1 ( s ) = T ( x , x − s ω ) ( P a μ a L e ( x − s ω , ω ) 1 { ξ < P a } + P s μ s L s ( x − s ω , ω ) 1 { ξ ≥ P a } ) ( 9 ) ここで問題なのはP a P_a P a P s P_s P s μ a \mu_a μ a μ s \mu_s μ s P a P_a P a P s P_s P s
P a = μ a μ t P s = μ s μ t (10) \begin{aligned}
P_a &= \frac{\mu_a}{\mu_t} \\
P_s &= \frac{\mu_s}{\mu_t} \tag{10}
\end{aligned} P a P s = μ t μ a = μ t μ s ( 1 0 ) μ t = μ a + μ s \mu_t = \mu_a + \mu_s μ t = μ a + μ s P a P_a P a P s P_s P s [ 0 , 1 ] [0, 1] [ 0 , 1 ]
他にもP a P_a P a μ a L e \mu_a L_e μ a L e
吸収イベントが選択された場合はT μ a L e P a T\frac{\mu_a L_e}{P_a} T P a μ a L e T μ s L s P s T\frac{\mu_s L_s}{P_s} T P s μ s L s
L e L_e L e L s L_s L s L s L_s L s
L s L_s L s L s L_s L s
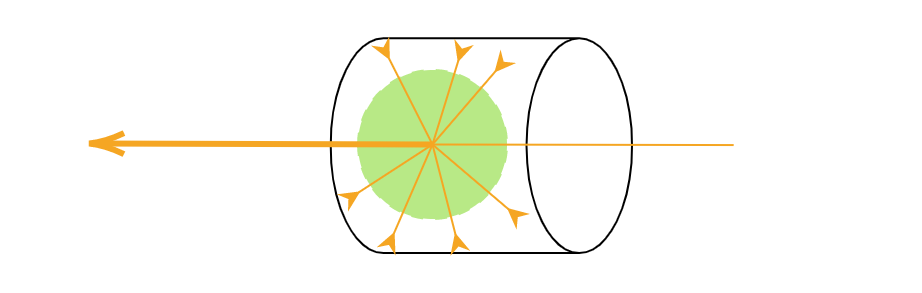
L s ( x , ω ⃗ ) = ∫ S 2 f p ( ω ⃗ , ω ⃗ ′ ) L i ( x , ω ⃗ ′ ) d σ ( ω ⃗ ′ ) L_s(x, \vec{\omega}) = \int_{\mathcal{S}^2} f_p(\vec{\omega}, \vec{\omega}')L_i(x, \vec{\omega}')d\sigma(\vec{\omega}') L s ( x , ω ) = ∫ S 2 f p ( ω , ω ′ ) L i ( x , ω ′ ) d σ ( ω ′ ) これもモンテカルロ積分で評価することを考えます。 ランダムな方向を表す確率変数をD : Ω → S 2 D: \Omega \to \mathcal{S}^2 D : Ω → S 2 D D D p D ( ω ⃗ ) p_{D}(\vec{\omega}) p D ( ω ) D D D ω ⃗ i ′ \vec{\omega}_i' ω i ′ N L s N_{L_s} N L s L s L_s L s
L s ^ ( x , ω ⃗ ) = 1 N L s ∑ i = 1 N L s f p ( ω ⃗ , ω ⃗ i ′ ) L i ( x , ω ⃗ i ′ ) p D ( ω ⃗ i ′ ) (11) \widehat{L_s}(x, \vec{\omega}) = \frac{1}{N_{L_s}}\sum_{i=1}^{N_{L_s}}\frac{f_p(\vec{\omega}, \vec{\omega}_i')L_i(x, \vec{\omega}_i')}{p_D(\vec{\omega}_i')} \tag{11} L s ( x , ω ) = N L s 1 i = 1 ∑ N L s p D ( ω i ′ ) f p ( ω , ω i ′ ) L i ( x , ω i ′ ) ( 1 1 ) 重点的サンプリングを考えると、D D D f p f_p f p
∫ S 2 f p ( ω ⃗ , ω ⃗ ′ ) d σ ( ω ⃗ ′ ) = 1 \int_{\mathcal{S}^2} f_p(\vec{\omega}, \vec{\omega}')d\sigma(\vec{\omega}') = 1 ∫ S 2 f p ( ω , ω ′ ) d σ ( ω ′ ) = 1 つまり、f p f_p f p p D ( ω ⃗ ′ ) p_D(\vec{\omega}') p D ( ω ′ )
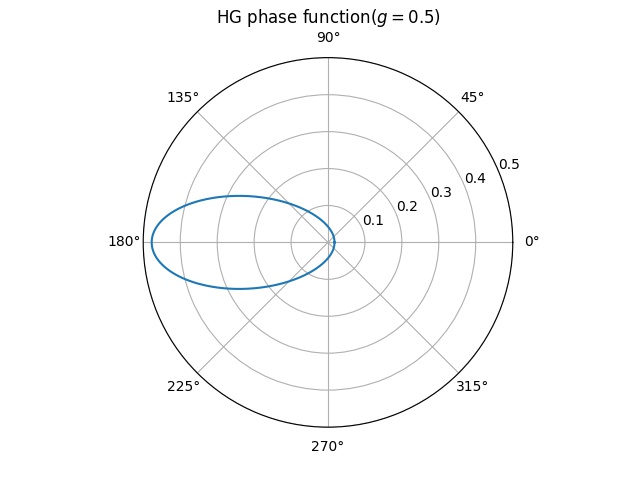
p D ( ω ⃗ ′ ) = f p ( ω ⃗ , ω ⃗ ′ ) p_D(\vec{\omega}') = f_p(\vec{\omega}, \vec{\omega}') p D ( ω ′ ) = f p ( ω , ω ′ ) レンダリングでは位相関数として以下の Henyey-Greenstein phase function がよく使われます。以下HG位相関数と呼ぶことにします。
θ \theta θ ω ⃗ \vec{\omega} ω ω ⃗ ′ \vec{\omega}' ω ′ g g g
f p ( ω ⃗ , ω ⃗ ′ ) = 1 4 π 1 − g 2 ( 1 + g 2 + 2 g cos θ ) 3 2 f_p(\vec{\omega}, \vec{\omega}') = \frac{1}{4\pi}\frac{1 - g^2}{(1 + g^2 + 2g\cos\theta)^\frac{3}{2}} f p ( ω , ω ′ ) = 4 π 1 ( 1 + g 2 + 2 g cos θ ) 2 3 1 − g 2 g = 0.5の場合のHG位相関数 HG位相関数では逆関数法を用いて位相関数からの方向サンプリングが行えます。ここではそれについては解説しませんが、気になる方は以下のPBRTのページが参考になります。
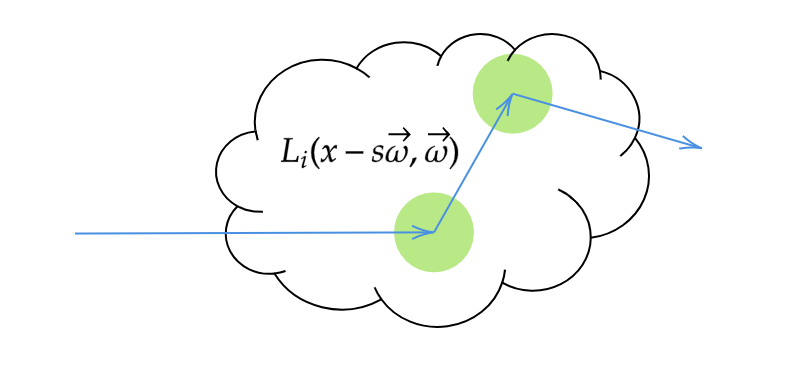
位相関数を用いて方向ω ⃗ i ′ \vec{\omega}_i' ω i ′ L i ( x , ω ⃗ i ′ ) L_i(x, \vec{\omega}_i') L i ( x , ω i ′ ) x x x ω ⃗ i ′ \vec{\omega}_i' ω i ′ L i L_i L i
VREの再帰的な適用 式(11)は方向サンプルを複数個取る一般的な場合も含めて記述していますが、実際にはN L s = 1 N_{L_s} = 1 N L s = 1 L s L_s L s N L s > 1 N_{L_s} > 1 N L s > 1 N L s = 1 N_{L_s} = 1 N L s = 1
L s ^ ( x , ω ⃗ ) = f p ( ω ⃗ , ω ⃗ i ′ ) L i ( x , ω ⃗ ′ ) p D ( ω ⃗ i ′ ) (12) \widehat{L_s}(x, \vec{\omega}) = \frac{f_p(\vec{\omega}, \vec{\omega}_i')L_i(x, \vec{\omega}')}{p_D(\vec{\omega}_i')} \tag{12} L s ( x , ω ) = p D ( ω i ′ ) f p ( ω , ω i ′ ) L i ( x , ω ′ ) ( 1 2 ) 次は残りのT e r m 2 \mathrm{Term2} T e r m 2
T e r m 2 \mathrm{Term2} T e r m 2 T e r m 2 \mathrm{Term2} T e r m 2
T e r m 2 = T ( x , x − t ω ⃗ ) L ( x − t ω ⃗ , ω ⃗ ) \mathrm{Term2} = T(x, x - t\vec{\omega})L(x - t\vec{\omega}, \vec{\omega}) T e r m 2 = T ( x , x − t ω ) L ( x − t ω , ω ) T T T
T ( x , x − t ω ⃗ ) = e − μ t t T(x, x - t\vec{\omega}) = e^{-\mu_t t} T ( x , x − t ω ) = e − μ t t L ( x − t ω ⃗ , ω ⃗ ) L(x - t\vec{\omega}, \vec{\omega}) L ( x − t ω , ω ) L ( x − t ω ⃗ , ω ⃗ ) L(x - t\vec{\omega}, \vec{\omega}) L ( x − t ω , ω )
媒質の終端が別の媒質の場合 媒質の終端の隣が真空の場合はレンダリング方程式を使ってL ( x − t ω ⃗ , ω ⃗ ) L(x - t\vec{\omega}, \vec{\omega}) L ( x − t ω , ω ) L ( x − t ω ⃗ , ω ⃗ ) L(x - t\vec{\omega}, \vec{\omega}) L ( x − t ω , ω )
媒質の終端が真空の場合 これまで説明してきたことをまとめると、一様媒質の場合のVREのモンテカルロ積分は以下のように書けます。
s s s ξ \xi ξ [ 0 , 1 ] [0, 1] [ 0 , 1 ]
L ^ ( x , ω ⃗ ) = T ( x , x − s ω ⃗ ) ( μ a L e ( x − s ω ⃗ , ω ⃗ ) P a 1 { ξ < P a } + μ s L s ^ ( x − s ω ⃗ , ω ⃗ ) P s 1 { ξ ≥ P a } ) p S ( s ) 1 { s < t } + T ( x , x − t ω ⃗ ) L ( x − t ω ⃗ , ω ⃗ ) P ( S ≥ t ) 1 { s ≥ t } (13) \begin{aligned}
\widehat{L}(x, \vec{\omega}) &= \frac{T(x, x - s\vec{\omega})\bigg( \frac{\mu_a L_e(x - s\vec{\omega}, \vec{\omega})}{P_a}\mathbb{1}_{\{\xi < P_a\}} + \frac{\mu_s\widehat{L_s}(x - s\vec{\omega}, \vec{\omega})}{P_s}\mathbb{1}_{\{\xi \ge P_a\}}\bigg)}{p_S(s)}\mathbb{1}_{\{s < t\}} \\
&+ \frac{T(x, x - t\vec{\omega})L(x - t\vec{\omega}, \vec{\omega})}{P(S \ge t)}\mathbb{1}_{\{s \ge t\}} \tag{13}
\end{aligned} L ( x , ω ) = p S ( s ) T ( x , x − s ω ) ( P a μ a L e ( x − s ω , ω ) 1 { ξ < P a } + P s μ s L s ( x − s ω , ω ) 1 { ξ ≥ P a } ) 1 { s < t } + P ( S ≥ t ) T ( x , x − t ω ) L ( x − t ω , ω ) 1 { s ≥ t } ( 1 3 ) L s ^ ( x − s ω ⃗ , ω ⃗ ) = f p ( ω ⃗ , ω ⃗ ′ ) L i ( x − s ω ⃗ , ω ⃗ ′ ) p D ( ω ⃗ ′ ) (14) \widehat{L_s}(x - s\vec{\omega}, \vec{\omega}) = \frac{f_p(\vec{\omega}, \vec{\omega}')L_i(x - s\vec{\omega}, \vec{\omega}')}{p_D(\vec{\omega}')} \tag{14} L s ( x − s ω , ω ) = p D ( ω ′ ) f p ( ω , ω ′ ) L i ( x − s ω , ω ′ ) ( 1 4 ) T T T p S p_S p S
透過率: T ( x , x − s ω ⃗ ) = e − μ t s T(x, x - s\vec{\omega}) = e^{-\mu_t s} T ( x , x − s ω ) = e − μ t s
距離S S S p S ( s ) = μ t T ( x , x − s ω ⃗ ) p_S(s) = \mu_t T(x, x - s\vec{\omega}) p S ( s ) = μ t T ( x , x − s ω )
T e r m 2 \mathrm{Term2} T e r m 2 P ( S ≥ t ) = 1 − F S ( S < t ) = T ( x , x − t ω ⃗ ) P(S \ge t) = 1 - F_S(S < t) = T(x, x - t\vec{\omega}) P ( S ≥ t ) = 1 − F S ( S < t ) = T ( x , x − t ω ) 吸収イベントを選択する確率: P a = μ a μ t P_a = \frac{\mu_a}{\mu_t} P a = μ t μ a
散乱イベントを選択する確率: P s = μ s μ t P_s = \frac{\mu_s}{\mu_t} P s = μ t μ s
散乱方向D D D P D ( ω ⃗ ′ ) = f p ( ω ⃗ , ω ⃗ ′ ) P_D(\vec{\omega}') = f_p(\vec{\omega}, \vec{\omega}') P D ( ω ′ ) = f p ( ω , ω ′ )
これらを式(13), 式(14)に代入してあげると以下のようになります。
L ^ ( x , ω ⃗ ) = ( L e ( x − s ω ⃗ , ω ⃗ ) 1 { ξ < P a } + L i ( x − s ω ⃗ , ω ⃗ ′ ) 1 { ξ ≥ P a } ) 1 { s < t } + L ( x − t ω ⃗ , ω ⃗ ) 1 { s ≥ t } (15) \begin{aligned}
\widehat{L}(x, \vec{\omega}) &= \bigg(L_e(x - s\vec{\omega}, \vec{\omega})\mathbb{1}_{\{\xi < P_a\}} + L_i(x - s\vec{\omega}, \vec{\omega}')\mathbb{1}_{\{\xi \ge P_a\}}\bigg)\mathbb{1}_{\{s < t\}} \\
&+ L(x - t\vec{\omega}, \vec{\omega})\mathbb{1}_{\{s \ge t\}} \tag{15}
\end{aligned} L ( x , ω ) = ( L e ( x − s ω , ω ) 1 { ξ < P a } + L i ( x − s ω , ω ′ ) 1 { ξ ≥ P a } ) 1 { s < t } + L ( x − t ω , ω ) 1 { s ≥ t } ( 1 5 ) T T T p S p_S p S p S p_S p S P a , P s P_a, P_s P a , P s p D p_D p D
アルゴリズム的には以下のようにまとめられます。
距離s s s
s < t s < t s < t
[ 0 , 1 ] [0, 1] [ 0 , 1 ] ξ \xi ξ ξ < P a \xi < P_a ξ < P a L e ( x − s ω ⃗ , ω ⃗ ) L_e(x - s\vec{\omega}, \vec{\omega}) L e ( x − s ω , ω ) ξ ≥ P a \xi \ge P_a ξ ≥ P a ω ⃗ ′ \vec{\omega}' ω ′ x − s ω ⃗ x - s\vec{\omega} x − s ω ω ⃗ ′ \vec{\omega}' ω ′
s ≥ t s \ge t s ≥ t L ( x − t ω ⃗ , ω ⃗ ) L(x - t\vec{\omega}, \vec{\omega}) L ( x − t ω , ω ) x − t ω ⃗ x - t\vec{\omega} x − t ω
媒質が発光しない場合(L e = 0 L_e = 0 L e = 0
この場合、散乱イベントを選択する確率は常に1になります。
P a = 0 P s = 1 \begin{aligned}
P_a &= 0 \\
P_s &= 1
\end{aligned} P a P s = 0 = 1 式(13), 式(14)にこれを代入してあげると以下のようになります。
L ^ ( x , ω ⃗ ) = μ s μ t L i ( x − s ω ⃗ , ω ⃗ ′ ) 1 { s < t } + L ( x − t ω ⃗ , ω ⃗ ) 1 { s ≥ t } (16) \begin{aligned}
\widehat{L}(x, \vec{\omega}) &= \frac{\mu_s}{\mu_t}L_i(x - s\vec{\omega}, \vec{\omega}')\mathbb{1}_{\{s < t\}} \\
&+ L(x - t\vec{\omega}, \vec{\omega})\mathbb{1}_{\{s \ge t\}} \tag{16}
\end{aligned} L ( x , ω ) = μ t μ s L i ( x − s ω , ω ′ ) 1 { s < t } + L ( x − t ω , ω ) 1 { s ≥ t } ( 1 6 ) 発光がある場合と比べるとμ s μ t \frac{\mu_s}{\mu_t} μ t μ s L i L_i L i 単一散乱アルベド(Single-scattering albedo) と呼ばれます。
VREのモンテカルロ積分は複雑に見えますが、最終的に出てくるアルゴリズムは意外とシンプルです。個人的には一見数値計算が不可能に見えるVREがこのような確率論的な手法で数値計算出来てしまうことに面白さを感じます。モンテカルロレイトレーシングは確率論の応用として非常に面白い分野だと思います。
こういった計算は原子核物理学の分野でも使われているそうです。そっちの数値計算もいつかやってみたいですね。
今回は一様媒質の場合を扱いましたが、非一様媒質の場合も実はNull collision particleという、衝突しても何もしない粒子で隙間を埋めてあげることで一様媒質に帰着させて計算できます(Delta Tracking )。そのため、非一様媒質に対するモンテカルロレイトレーシングをやる場合でも今回の内容は理論的な基礎になります。
また、今回は吸収係数/散乱係数が波長非依存であると仮定して式の導出を行ってきました。これだと色付きの媒質がレンダリングできないという問題があります。波長依存の場合は波長を最初にランダムに選び、その波長で自由行程サンプリング、吸収/散乱イベントサンプリングを行ったりします。
非一様媒質の場合や吸収係数/散乱係数が波長依存の場合、実装方法などについてもそのうち別の記事で紹介していきたいと思います。