モンテカルロレイトレーシングでCorrelated Multi Jittered Sampling(CMJ)を使う

この記事はレイトレ合宿8アドベントカレンダー 8/14日枠の記事です。今回は自分のレンダラーで使用している乱数についての記事を書いてみました。この記事では手法の解説は最小限に抑え、実際の使い方にフォーカスしています。

TL;DR

CMJでお手軽に2次元層化サンプリング
BxDFサンプリング(1D), 反射方向のサンプリング(2D)などの個々のサンプリングでCMJを利用
適切に使用することでモンテカルロ積分の収束が早くなる

Correlated Multi Jittered Sampling(CMJ)

Correlated Multi Jittered Sampling(CMJ)はKensler[2013]による層化サンプリングの手法です。今、乱数の値の空間として $[0, 1]^d$ を考えた時に, CMJは $[0, 1]^2$ で出来るだけ一様に分布するように乱数を生成することが出来ます。

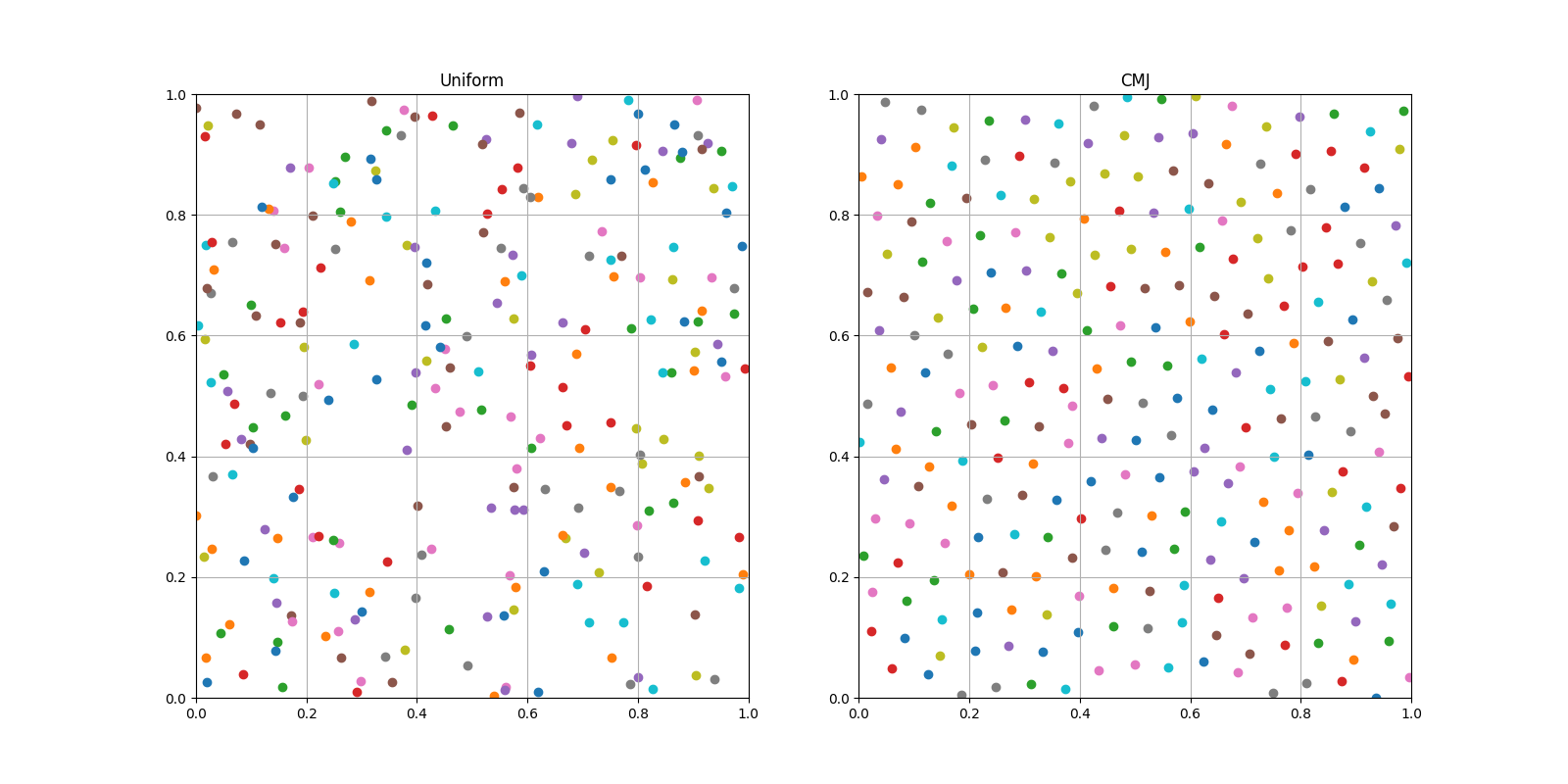
CMJの基本的なアイデアは $[0, 1]^2$ の空間を $M \times N$ の格子に分割し、各格子の中で乱数生成を行うことです(層化サンプリング)。CMJでは各格子中での乱数生成の仕方を工夫することで、モンテカルロ積分の収束を早めたり、構造的アーティファクトが出にくいようになっています。

論文中には乱数生成を行う疑似コード(Listing 3, 4, 5, 6)があり、それを使うことで簡単にCMJを使うことが出来ます。C++でCMJを行うコードを書くと以下のようになります。

unsigned int cmj_permute(unsigned int i, unsigned int l,
                            unsigned int p) {
  unsigned int w = l - 1;
  w |= w >> 1;
  w |= w >> 2;
  w |= w >> 4;
  w |= w >> 8;
  w |= w >> 16;
  do {
    i ^= p;
    i *= 0xe170893d;
    i ^= p >> 16;
    i ^= (i & w) >> 4;
    i ^= p >> 8;
    i *= 0x0929eb3f;
    i ^= p >> 23;
    i ^= (i & w) >> 1;
    i *= 1 | p >> 27;
    i *= 0x6935fa69;
    i ^= (i & w) >> 11;
    i *= 0x74dcb303;
    i ^= (i & w) >> 2;
    i *= 0x9e501cc3;
    i ^= (i & w) >> 2;
    i *= 0xc860a3df;
    i &= w;
    i ^= i >> 5;
  } while (i >= l);
  return (i + p) % l;
}

float cmj_randfloat(unsigned int i, unsigned int p) {
  i ^= p;
  i ^= i >> 17;
  i ^= i >> 10;
  i *= 0xb36534e5;
  i ^= i >> 12;
  i ^= i >> 21;
  i *= 0x93fc4795;
  i ^= 0xdf6e307f;
  i ^= i >> 17;
  i *= 1 | p >> 18;
  return i * (1.0f / (1ULL << 32));
}

// s: 乱数インデックス
// m: 横方向の分割数
// n: 縦方向の分割数
// p: 乱数パターン
float2 cmj(unsigned int s, unsigned int m,
                                   unsigned int n, unsigned int p) {
  s = cmj_permute(s, m * n, p * 0x51633e2d); // Scan line orderを崩す
  unsigned int sx = cmj_permute(s % m, m, p * 0xa511e9b3);
  unsigned int sy = cmj_permute(s / m, n, p * 0x63d83595);
  float jx = cmj_randfloat(s, p * 0xa399d265);
  float jy = cmj_randfloat(s, p * 0x711ad6a5);
  return make_float2((s % m + (sy + jx) / n) / m, (s / m + (sx + jy) / m) / n);
}

論文中のCMJの実装(Listing 5)では、乱数がScan line orderで整列した順番で出るようになっていますが、上の実装ではsに対してcmj_permuteを行うことで、整列を崩しています。

モンテカルロ積分は $N$ をサンプル数とすると、収束のオーダーが $O(\frac{1}{\sqrt{N}})$ と遅いですが、層化サンプリングや準モンテカルロ法(QMC)を利用することで収束のオーダーを改善出来ることが知られています。モンテカルロレイトレーシングではレンダリング方程式のモンテカルロ積分を行うので、ここにCMJを利用することで画像の収束が早まることが期待されます。

CMJをレンダラーで使う

モンテカルロレイトレーシングにおいてはBxDFのサンプリング(1D), 反射方向のサンプリング(2D), 光源サンプリング(2D)などを各交差点で行う必要があるため、1つのパスを作るのに高次元の乱数が必要となります。

CMJで生成出来るのは2次元の乱数ですが、モンテカルロレイトレーシングにおいてはBxDFサンプリング、反射方向のサンプリングなど個々のサンプリングにおいては高々2次元までの乱数しか必要とされないことが多いです。そのため個々のサンプリングにおいてCMJを利用することが出来ます。

このようにすることで、個々のサンプリングにおいては層化されたサンプルを得ることが出来るようになります。一方で1つのパス全体(高次元の乱数として)を見た時にはもはや層化されているとは言えませんが、少なくとも普通の乱数を使うよりは良いはずです。

実際にCMJを使う上では幾つか注意する点があります。

まず、sとpの入力に注意します。sは乱数のインデックスに対応し、この値を0から $M \times N$ まで増やしていくことで $[0, 1]^2$ で一様に分布する乱数列を得ることが出来ます。一方でpは乱数パターン(seed)に対応し、この値を変えることで異なる乱数列を得ることが出来ます。

これを踏まえると、sは以下のように計算できます。

// n_spp: サンプル数
// CMJ_M: M
// CMJ_N: N
unsigned int s = n_spp % (CMJ_M * CMJ_N);

一方でpは各ピクセル, 個々のサンプリングにおいて異なる値となってほしいので, 以下のように計算します。

// https://www.shadertoy.com/view/XlGcRh
uint xxhash32(const uint4& p)
{
  const uint PRIME32_2 = 2246822519U, PRIME32_3 = 3266489917U;
  const uint PRIME32_4 = 668265263U, PRIME32_5 = 374761393U;
  uint h32 = p.w + PRIME32_5 + p.x * PRIME32_3;
  h32 = PRIME32_4 * ((h32 << 17) | (h32 >> (32 - 17)));
  h32 += p.y * PRIME32_3;
  h32 = PRIME32_4 * ((h32 << 17) | (h32 >> (32 - 17)));
  h32 += p.z * PRIME32_3;
  h32 = PRIME32_4 * ((h32 << 17) | (h32 >> (32 - 17)));
  h32 = PRIME32_2 * (h32 ^ (h32 >> 15));
  h32 = PRIME32_3 * (h32 ^ (h32 >> 13));
  return h32 ^ (h32 >> 16);
}

// pixel_idx: ピクセルのインデックス
// dimension: 乱数の次元
// seed: seed値
unsigned int p =
    xxhash32(make_uint4(n_spp / (CMJ_M * CMJ_N), pixel_idx, dimension, seed));

dimensionはCMJを呼び出すたびにincrementさせます。このようにpを計算することで、個々のピクセル、個々のサンプリングにおいて異なる乱数列を得ることが出来ます。

もう一つの注意点として、CMJの格子分割数 $M, N$ は出来るだけ $M \times N$ がサンプル数と近い値になるように設定するべきです。そうでないと、一部の格子のみでサンプルが生成されるので、生成された乱数列は $[0, 1]^2$ の一部分しか埋めなくなり、モンテカルロ積分の収束が悪くなります。

レンダリング

CMJを使ってコーネルボックスをレンダリングし、普通の乱数を使った場合と比較してみます。

まずは直接照明のみで試してみます。サンプル数は16, CMJの格子分割数はサンプル数に合わせて4x4とします。

画像を見ると明らかにCMJを使ったほうがノイズが少ないことが分かります。定量的にもリファレンスと比較した時のRMSEの値が小さくなっており、CMJによって収束が早まっている様子が分かります。

ここでCMJの格子分割数を16x16に変えてみます。今、サンプル数は16しかないので、これによってCMJで生成される乱数は分割された格子の一部のみを埋めるようになるので、4x4の場合よりもノイズが増えることが期待されます。この設定でレンダリングしてみると以下のようになります。

4x4の場合と比べて明らかにノイズが増えてしまっていることが分かります。RMSEの値も16x16の場合では普通の乱数と近い値になってしまっています。この結果から、CMJの格子分割数 $M, N$ は $M \times N \approx N_{spp}$ となるように設定するべきであることが分かります。

次に間接照明も含めた場合で試してみます。サンプル数は16, CMJの格子分割数は4x4です。

直接照明の場合と比べると効果は低減していますが、CMJを使ったほうがノイズが少ないことが分かります。間接照明の場合は1つのパスを作るのに高次元の乱数(> 2次元)を使うので、CMJを使った手法では完全な層化サンプリングは行えていませんが、それでも普通の乱数を使う場合よりは良いことが分かります。

発展手法

CMJの発展手法としては以下のようなものがあります。

特にOrthogonal Array Samplingは2次元に限定されていたCMJを $n$ 次元に一般化した手法です。高次元の場合でも層化されたサンプルが得られるので、CMJよりモンテカルロ積分の収束が早くなることが期待されます。

また、関連する内容としてqさんが魔法陣を利用したサンプリングについての記事をアドカレに書いてくださっています。こちらも是非覗いてみてください。

https://ykozw.github.io/post/magicsquare.html

最後に

レンダリング手法を変えずに、乱数を変えるだけでノイズが減ってくれるので最高です。特に最近は出来るだけ少ないサンプル数で綺麗な画像を作ることが求められる場面が多くなっているので、こういったサンプリング周りにこだわることは価値があると思います。

References

Correlated Multi-Jittered Sampling