この記事はレイトレアドベントカレンダー2021 25日目の記事です。この記事では吸収/散乱係数が波長依存の媒質に対するモンテカルロレイトレーシングの方法について解説しています。前提として24日目の記事 の内容は知っているものとします。
最初に波長をランダムにサンプリングする
サンプリングした波長で自由行程サンプリング/吸収・散乱イベントサンプリングを行う
全波長分の寄与をMISをしつつ一気に計算する
世の中にある多くの媒質は色がついているように見えます。例えば大気や水は青っぽく見えます。これは吸収/散乱係数の大きさが波長によって異なるためです。
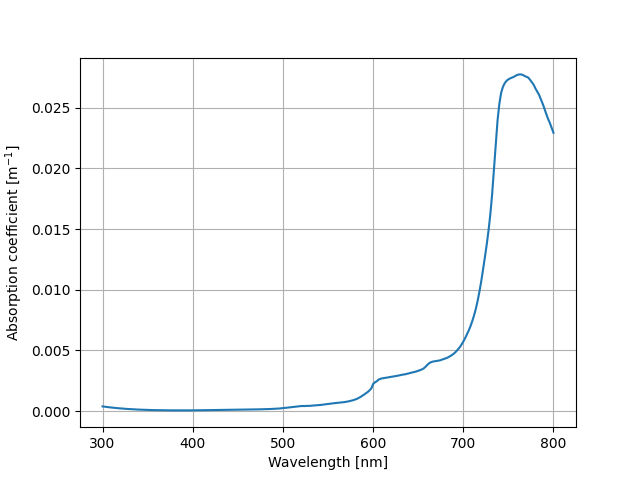
以下は水の吸収係数を表すグラフです。横軸が波長、縦軸が吸収係数です。(データは H. Buiteveld and J. M. H. Hakvoort and M. Donze, "The optical properties of pure water," in SPIE Proceedings on Ocean Optics XII, edited by J. S. Jaffe, 2258, 174--183, (1994) より)
水の吸収係数 波長が長い光(赤)は吸収されやすく、波長が短い光(青)は吸収されにくいことが分かります。赤い光が吸収されてしまうので水は青く見えるわけです。
スペクトルレンダラーでは上記の曲線をそのまま吸収係数として使うことが出来ます。RGBレンダラーでは上記の曲線から赤, 緑, 青に対応する波長のデータだけを抜き出して、3次元ベクトルとして吸収係数を表現すれば良いでしょう。
理論的な拠り所を得るために、ここでは吸収/散乱係数が波長依存の場合のボリュームレンダリング方程式(以降VREと呼びます)について考えます。
吸収/散乱係数が波長非依存の場合のVREは以下のような形でした。
L ( x , ω ⃗ ) = ∫ 0 t T ( x , x − s ω ⃗ ) ( μ a ( x − s ω ⃗ ) L e ( x − s ω ⃗ , ω ⃗ ) + μ s ( x − s ω ⃗ ) L s ( x − s ω ⃗ , ω ⃗ ) ) d s + T ( x , x − t ω ⃗ ) L ( x − t ω ⃗ , ω ⃗ ) \begin{aligned}
L(x, \vec{\omega}) &= \int_0^t T(x, x - s\vec{\omega})\bigg( \mu_a(x - s\vec{\omega})L_e(x - s\vec{\omega}, \vec{\omega}) + \mu_s(x - s\vec{\omega})L_s(x - s\vec{\omega}, \vec{\omega}) \bigg)ds \\
&+ T(x, x - t\vec{\omega})L(x - t\vec{\omega}, \vec{\omega})
\end{aligned} L ( x , ω ) = ∫ 0 t T ( x , x − s ω ) ( μ a ( x − s ω ) L e ( x − s ω , ω ) + μ s ( x − s ω ) L s ( x − s ω , ω ) ) d s + T ( x , x − t ω ) L ( x − t ω , ω ) これを吸収/散乱係数が波長依存の形の式に変えるには、波長を表すλ \lambda λ
L ( x , ω ⃗ , λ ) = ∫ 0 t T ( x , x − s ω ⃗ , λ ) ( μ a ( x − s ω ⃗ , λ ) L e ( x − s ω ⃗ , ω ⃗ , λ ) + μ s ( x − s ω ⃗ , λ ) L s ( x − s ω ⃗ , ω ⃗ , λ ) ) d s + T ( x , x − t ω ⃗ , λ ) L ( x − t ω ⃗ , ω ⃗ , λ ) (1) \begin{aligned}
L(x, \vec{\omega}, \lambda) &= \int_0^t T(x, x - s\vec{\omega}, \lambda)\bigg( \mu_a(x - s\vec{\omega}, \lambda)L_e(x - s\vec{\omega}, \vec{\omega}, \lambda) + \mu_s(x - s\vec{\omega}, \lambda)L_s(x - s\vec{\omega}, \vec{\omega}, \lambda) \bigg)ds \\
&+ T(x, x - t\vec{\omega}, \lambda)L(x - t\vec{\omega}, \vec{\omega}, \lambda) \tag{1}
\end{aligned} L ( x , ω , λ ) = ∫ 0 t T ( x , x − s ω , λ ) ( μ a ( x − s ω , λ ) L e ( x − s ω , ω , λ ) + μ s ( x − s ω , λ ) L s ( x − s ω , ω , λ ) ) d s + T ( x , x − t ω , λ ) L ( x − t ω , ω , λ ) ( 1 ) これが吸収/散乱係数が波長依存の場合のVREです。これを数値計算することがこの記事の目標になります。
式(1)は波長ごとの放射輝度(分光放射輝度)を計算する式になっています。レンダラーで分光放射輝度をRGBの画像にするためには、以下のように等色関数を用いて分光放射輝度を一度XYZ色空間に変換し、その後XYZをRGBに変換します。
L ( λ ) L(\lambda) L ( λ ) x ˉ ( λ ) \bar{x}(\lambda) x ˉ ( λ ) y ˉ ( λ ) \bar{y}(\lambda) y ˉ ( λ ) z ˉ ( λ ) \bar{z}(\lambda) z ˉ ( λ )
X = ∫ 0 ∞ L ( λ ) x ˉ ( λ ) d λ Y = ∫ 0 ∞ L ( λ ) y ˉ ( λ ) d λ Z = ∫ 0 ∞ L ( λ ) z ˉ ( λ ) d λ \begin{aligned}
X &= \int_0^{\infty} L(\lambda)\bar{x}(\lambda) d\lambda \\
Y &= \int_0^{\infty} L(\lambda)\bar{y}(\lambda) d\lambda \\
Z &= \int_0^{\infty} L(\lambda)\bar{z}(\lambda) d\lambda
\end{aligned} X Y Z = ∫ 0 ∞ L ( λ ) x ˉ ( λ ) d λ = ∫ 0 ∞ L ( λ ) y ˉ ( λ ) d λ = ∫ 0 ∞ L ( λ ) z ˉ ( λ ) d λ これらの積分は波長をランダムサンプリングすることで、モンテカルロ積分を用いて計算することが出来ます。
N N N L L L p L ( λ ) p_{L}(\lambda) p L ( λ ) L L L
X = 1 N ∑ i = 1 N L ( λ i ) x ˉ ( λ i ) p L ( λ i ) Y = 1 N ∑ i = 1 N L ( λ i ) y ˉ ( λ i ) p L ( λ i ) Z = 1 N ∑ i = 1 N L ( λ i ) z ˉ ( λ i ) p L ( λ i ) (2) \begin{aligned}
X &= \frac{1}{N}\sum_{i=1}^N \frac{L(\lambda_i)\bar{x}(\lambda_i)}{p_L(\lambda_i)} \\
Y &= \frac{1}{N}\sum_{i=1}^N \frac{L(\lambda_i)\bar{y}(\lambda_i)}{p_L(\lambda_i)} \\
Z &= \frac{1}{N}\sum_{i=1}^N \frac{L(\lambda_i)\bar{z}(\lambda_i)}{p_L(\lambda_i)} \tag{2}
\end{aligned} X Y Z = N 1 i = 1 ∑ N p L ( λ i ) L ( λ i ) x ˉ ( λ i ) = N 1 i = 1 ∑ N p L ( λ i ) L ( λ i ) y ˉ ( λ i ) = N 1 i = 1 ∑ N p L ( λ i ) L ( λ i ) z ˉ ( λ i ) ( 2 ) もっと詳しい話はちょうどアドカレで別の方が書いてくださっているので、そちらも合わせて参考にして下さい。
式(2)から、スペクトルレンダラーの実装ではまず最初に波長をランダムに選び、その波長で分光放射輝度を計算すれば良いです。この場合式(1)の評価は単純に吸収/散乱係数をサンプリングした波長に対応する値にして評価すれば良いだけなので、特に難しいことはありません。
しかしこの方法はただでさえノイズが多くなりがちなモンテカルロレイトレーシングによる計算が、波長のランダムサンプリングによって色ノイズが追加で加わり、収束が遅くなってしまうという問題があります。
波長のランダムサンプリングによる色ノイズ 大抵のシーンのレンダリングではスペクトルレンダリングまでやらなくても、RGBによるレンダリングだけで十分なことも多いです。しかし、この方法だとRGBレンダリングをやる場合でもR, G, Bの各成分をランダムにサンプリングしなければならないので効率が悪いです。
そこで、波長はランダムにサンプリングするけれども、その波長だけではなくて全波長分の寄与を一気に計算してしまうという方法を考えます。これが次に紹介する Hero wavelength sampling です。
Hero wavelength sampling はWilkie, Alexander, et alによって2014年に導入されたスペクトルレンダリングの手法です。Hero wavelength samplingではランダムにサンプリングされた波長でパスの構築をした後、そのパスの寄与をMulti importance sampling(MIS) を使いつつ全波長分一気に計算するということを行います。そのため単一波長だけで寄与を計算していく場合よりも色ノイズが少なくなります。
以下の画像はRGBレンダリングにおいて左が単一波長でレンダリングした場合、右がHero wavelength samplingでレンダリングした場合です。Hero wavelength samplingの方が色ノイズが減っているのが分かると思います。スペクトルレンダリングだと差はさらに顕著になるはずです。
単一波長とHero wavelength samplingの比較 MISは別々のサンプリング戦略から得られる寄与を良い感じに合算してくれるものですが、Hero wavelength samplingで言う戦略とは それぞれの波長で構築されるパスを別々のサンプリング戦略として見る という意味です。
例えばある色付きボリュームで波長をランダムに選び、モンテカルロレイトレーシングによってパスを構築したとします。ここで構築されるパスは別の波長を選んだ場合でも(確率密度が0でなければ)サンプリングできるはずです。つまり そのパスを作ることの出来るサンプリング戦略は波長の個数分だけ存在 することになります。
あるパスは別の波長を選んだ場合でも構築できる Hero wavelength samplingはガラスのように各波長で散乱方向が一意に定まるような材質では単一波長だけで寄与を計算した場合と計算効率が同じになってしまうのですが、ボリュームの場合は基本的にそのようなことが起こらないのでHero wavelength samplingを使ったほうが効率が良いです。ボリューム以外にもDiffuse面のスペクトルレンダリングなどにも有効だと思います。
今、分光放射輝度を計算したい対象の波長がλ 1 , λ 2 , ⋯ , λ C \lambda^1, \lambda^2, \cdots, \lambda^C λ 1 , λ 2 , ⋯ , λ C C C C C C C λ h \lambda^h λ h
N N N x ˉ i \bar{x}_i x ˉ i i i i w j ( x ˉ i , λ j ) w_j(\bar{x}_i, \lambda^j) w j ( x ˉ i , λ j ) j j j x ˉ i \bar{x}_i x ˉ i p ( x ˉ i , λ i h ) p(\bar{x}_i, \lambda_i^h) p ( x ˉ i , λ i h ) h h h x ˉ i \bar{x}_i x ˉ i
X = 1 N ∑ i = 1 N ∑ j = 1 C w j ( x ˉ i , λ j ) L ( x ˉ i , λ j ) p ( x ˉ i , λ i h ) x ˉ ( λ j ) (3) X = \frac{1}{N}\sum_{i=1}^N\sum_{j=1}^C w_j(\bar{x}_i, \lambda^j)\frac{L(\bar{x}_i, \lambda^j)}{p(\bar{x}_i, \lambda_i^h)}\bar{x}(\lambda^j) \tag{3} X = N 1 i = 1 ∑ N j = 1 ∑ C w j ( x ˉ i , λ j ) p ( x ˉ i , λ i h ) L ( x ˉ i , λ j ) x ˉ ( λ j ) ( 3 ) ここではX X X Y Y Y Z Z Z
RGBレンダリングの場合は次のようにR, G, Bの各成分を表すOne-hot vectorを導入することで、式(3)と同様の枠組みで記述できます。
δ i , j \delta_{i, j} δ i , j r g b i = ( δ 1 , i δ 2 , i δ 3 , i ) \boldsymbol{rgb}_i = \begin{pmatrix} \delta_{1, i} \\ \delta_{2, i} \\ \delta_{3, i} \end{pmatrix} r g b i = ⎝ ⎛ δ 1 , i δ 2 , i δ 3 , i ⎠ ⎞
R G B = 1 N ∑ i = 1 N ∑ j = 1 3 w j ( x ˉ i , λ j ) L ( x ˉ i , λ j ) p ( x ˉ i , λ i h ) r g b j (4) RGB = \frac{1}{N}\sum_{i=1}^N\sum_{j=1}^3 w_j(\bar{x}_i, \lambda^j)\frac{L(\bar{x}_i, \lambda^j)}{p(\bar{x}_i, \lambda_i^h)}\boldsymbol{rgb}_j \tag{4} R G B = N 1 i = 1 ∑ N j = 1 ∑ 3 w j ( x ˉ i , λ j ) p ( x ˉ i , λ i h ) L ( x ˉ i , λ j ) r g b j ( 4 ) ここでは式(3)をベースに話を進めていきます。
MISウェイトはバランスヒューリスティックを使うとすると、次のように計算できます。
w j ( x ˉ i , λ j ) = p j ( x ˉ i , λ j ) ∑ k = 1 C p k ( x ˉ i , λ j ) = p ( x ˉ i , λ i h ) ∑ k = 1 C p k ( x ˉ i , λ i h ) \begin{aligned}
w_j(\bar{x}_i, \lambda^j) &= \frac{p_j(\bar{x}_i, \lambda^j)}{\sum_{k=1}^C p_k(\bar{x}_i, \lambda^j)} \\
&= \frac{p(\bar{x}_i, \lambda_i^h)}{\sum_{k=1}^C p_k(\bar{x}_i, \lambda_i^h)}
\end{aligned} w j ( x ˉ i , λ j ) = ∑ k = 1 C p k ( x ˉ i , λ j ) p j ( x ˉ i , λ j ) = ∑ k = 1 C p k ( x ˉ i , λ i h ) p ( x ˉ i , λ i h ) 分子の確率密度は現在注目している戦略が与えられたパスを作る確率密度ですが、これは各j j j λ i h \lambda_i^h λ i h p ( x ˉ i , λ i h ) p(\bar{x}_i, \lambda_i^h) p ( x ˉ i , λ i h ) k k k x ˉ i \bar{x}_i x ˉ i λ i h \lambda_i^h λ i h
これを式(3)に代入すると次のような式を得ます。
P ( λ i h ) P(\lambda_i^h) P ( λ i h ) λ i h \lambda_i^h λ i h p ( x ˉ i ∣ λ k ) p(\bar{x}_i | \lambda_k) p ( x ˉ i ∣ λ k ) λ k \lambda_k λ k x ˉ i \bar{x}_i x ˉ i
X = 1 N ∑ i = 1 N ∑ j = 1 C L ( x ˉ i , λ j ) ∑ k = 1 C p k ( x ˉ i , λ i h ) x ˉ ( λ j ) = 1 N ∑ i = 1 N ∑ j = 1 C L ( x ˉ i , λ j ) ∑ k = 1 C P ( λ k ) p ( x ˉ i ∣ λ k ) x ˉ ( λ j ) (5) \begin{aligned}
X &= \frac{1}{N}\sum_{i=1}^N\sum_{j=1}^C \frac{L(\bar{x}_i, \lambda^j)}{\sum_{k=1}^C p_k(\bar{x}_i, \lambda_i^h)}\bar{x}(\lambda^j) \\
&= \frac{1}{N}\sum_{i=1}^N\sum_{j=1}^C \frac{L(\bar{x}_i, \lambda^j)}{\sum_{k=1}^C P(\lambda^k)p(\bar{x}_i | \lambda^k)}\bar{x}(\lambda^j) \tag{5}
\end{aligned} X = N 1 i = 1 ∑ N j = 1 ∑ C ∑ k = 1 C p k ( x ˉ i , λ i h ) L ( x ˉ i , λ j ) x ˉ ( λ j ) = N 1 i = 1 ∑ N j = 1 ∑ C ∑ k = 1 C P ( λ k ) p ( x ˉ i ∣ λ k ) L ( x ˉ i , λ j ) x ˉ ( λ j ) ( 5 ) MISウェイトの分子が相殺されて消えて、割とシンプルな形の式になりました。パスを作る波長λ i h \lambda_i^h λ i h
一様媒質の場合のVREのモンテカルロ積分に対してHero wavelength samplingを適用することを考えます。ここでは簡単のため散乱イベントが選択された時の寄与をHero wavelength samplingで計算することにします。
24日目の記事 の式(13)から、吸収/散乱係数が波長非依存の場合で散乱イベントが選択された時の寄与は以下のように書けるのでした。
L ^ ( x , ω ⃗ ) = T ( x , x − s ω ⃗ ) μ s L s ^ ( x − s ω ⃗ , ω ⃗ ) p S ( s ) P s (6) \widehat{L}(x, \vec{\omega}) = \frac{T(x, x - s\vec{\omega})\mu_s\widehat{L_s}(x - s\vec{\omega}, \vec{\omega})}{p_S(s)P_s} \tag{6} L ( x , ω ) = p S ( s ) P s T ( x , x − s ω ) μ s L s ( x − s ω , ω ) ( 6 ) この式をHero wavelength samplingを使って波長依存の吸収/散乱係数の場合に拡張していきます。C C C λ 1 , λ 2 , ⋯ , λ C \lambda^1, \lambda^2, \cdots, \lambda^C λ 1 , λ 2 , ⋯ , λ C λ h \lambda^h λ h L L L
まず式(5)の分子に当たる部分は、単純に評価をj j j λ j \lambda^j λ j
T ( x , x − s ω ⃗ , λ j ) μ s ( λ j ) L s ^ ( x − s ω ⃗ , ω ⃗ , λ j ) T(x, x - s\vec{\omega}, \lambda^j)\mu_s(\lambda^j)\widehat{L_s}(x - s\vec{\omega}, \vec{\omega}, \lambda^j) T ( x , x − s ω , λ j ) μ s ( λ j ) L s ( x − s ω , ω , λ j ) これを使うと式(6)は次のように書き換えられます。
∑ j = 1 C T ( x , x − s ω ⃗ , λ j ) μ s ( λ j ) L s ^ ( x − s ω ⃗ , ω ⃗ , λ j ) ∑ k = 1 C P ( λ k ) p ( x ˉ i ∣ λ k ) x ˉ ( λ j ) (7) \sum_{j=1}^C \frac{T(x, x - s\vec{\omega}, \lambda^j)\mu_s(\lambda^j)\widehat{L_s}(x - s\vec{\omega}, \vec{\omega}, \lambda^j)}{\sum_{k=1}^C P(\lambda^k)p(\bar{x}_i | \lambda^k)} \bar{x}(\lambda^j) \tag{7} j = 1 ∑ C ∑ k = 1 C P ( λ k ) p ( x ˉ i ∣ λ k ) T ( x , x − s ω , λ j ) μ s ( λ j ) L s ( x − s ω , ω , λ j ) x ˉ ( λ j ) ( 7 ) 次に式(7)の分母を計算していきます。
波長λ h \lambda^h λ h P λ h ( λ h ) P_{\lambda^h}(\lambda^h) P λ h ( λ h ) P ( λ k ) = P λ h ( λ h ) P(\lambda^k) = P_{\lambda^h}(\lambda^h) P ( λ k ) = P λ h ( λ h )
p ( x ˉ ∣ λ k ) p(\bar{x} | \lambda^k) p ( x ˉ ∣ λ k )
p ( x ˉ ∣ λ k ) = p S ( s , λ k ) P s ( λ k ) p S ( s , λ k ) = μ t ( λ k ) T ( x , x − s ω ⃗ , λ k ) P s ( λ k ) = μ s ( λ k ) μ t ( λ k ) \begin{aligned}
p(\bar{x} | \lambda^k) &= p_S(s, \lambda^k)P_s(\lambda^k) \\
p_S(s, \lambda^k) &= \mu_t(\lambda^k)T(x, x - s\vec{\omega}, \lambda^k) \\
P_s(\lambda^k) &= \frac{\mu_s(\lambda^k)}{\mu_t(\lambda^k)}
\end{aligned} p ( x ˉ ∣ λ k ) p S ( s , λ k ) P s ( λ k ) = p S ( s , λ k ) P s ( λ k ) = μ t ( λ k ) T ( x , x − s ω , λ k ) = μ t ( λ k ) μ s ( λ k ) これを式(7)に代入して最終的に次の式を得ます。
∑ j = 1 C T ( x , x − s ω ⃗ , λ j ) μ s ( λ j ) L s ^ ( x − s ω ⃗ , ω ⃗ , λ j ) P λ h ( λ h ) ∑ k = 1 C p S ( s , λ k ) P s ( λ k ) x ˉ ( λ j ) (8) \sum_{j=1}^C \frac{T(x, x - s\vec{\omega}, \lambda^j)\mu_s(\lambda^j)\widehat{L_s}(x - s\vec{\omega}, \vec{\omega}, \lambda^j)}{P_{\lambda^h}(\lambda^h)\sum_{k=1}^C p_S(s, \lambda^k)P_s(\lambda^k)} \bar{x}(\lambda^j) \tag{8} j = 1 ∑ C P λ h ( λ h ) ∑ k = 1 C p S ( s , λ k ) P s ( λ k ) T ( x , x − s ω , λ j ) μ s ( λ j ) L s ( x − s ω , ω , λ j ) x ˉ ( λ j ) ( 8 ) これが散乱イベントにHero wavelength samplingを適用した場合の寄与の計算方法です。
ここでは省略しますが、吸収イベントが選択された場合や、レイが媒質の終端に到達した場合も似たような計算によって式を導出できます。基本的には式(5)の分子分母をそれぞれの場合に置き換えていくだけです。
パスを構築する波長λ h \lambda^h λ h
まず最も簡単なのはC C C P λ h ( λ h ) P_{\lambda^h}(\lambda^h) P λ h ( λ h )
P λ h ( λ h ) = 1 C P_{\lambda^h}(\lambda^h) = \frac{1}{C} P λ h ( λ h ) = C 1 この方法はシンプルですが、吸収/散乱係数の波長依存が強い場合にはfireflyが出てしまうことがあります。これは式(8)の分子の値が大きく、分母の値が小さい場合などに発生します。
そこで、Wrenninge, Magnus, Ryusuke Villemin, and Christophe Heryによる論文 では波長を選択する確率を現在のレイのThroughputに比例させる方法が述べられています。これであれば式(8)の分子の値が大きい時には同時に分母の値も大きくなるので、fireflyは出にくくなります。
以下は表面化散乱のレンダリングにおいて波長を一様にサンプリングする場合(左)と、レイのThroughputに比例させてサンプリングする場合(右)の比較です。波長を一様にサンプリングする場合ではfireflyが出ていますが、Throughput比例の場合は綺麗にレンダリング出来ていることが分かります。
波長を一様にサンプリングする場合とThroughput比例の場合の比較 Throughput比例の場合はレイのThroughputをt ( λ k ) t(\lambda^k) t ( λ k ) P λ h ( λ h ) P_{\lambda^h}(\lambda^h) P λ h ( λ h )
P λ h ( λ h ) = t ( λ h ) ∑ k = 1 C t ( λ k ) P_{\lambda^h}(\lambda^h) = \frac{t(\lambda^h)}{\sum_{k=1}^C t(\lambda^k)} P λ h ( λ h ) = ∑ k = 1 C t ( λ k ) t ( λ h ) 逆関数法を用いればこのような離散確率分布からのサンプルを得ることができます。詳しくは以下のPBRTのページを参照して下さい。
@syoyo - 2018 年, ナウでヤングな path tracing based subsurface scattering を実装する Pharr, Matt, Wenzel Jakob, and Greg Humphreys. Physically based rendering: From theory to implementation. Morgan Kaufmann, 2016. H. Buiteveld and J. M. H. Hakvoort and M. Donze, "The optical properties of pure water," in SPIE Proceedings on Ocean Optics XII, edited by J. S. Jaffe, 2258, 174--183, (1994) Wilkie, Alexander, et al. "Hero wavelength spectral sampling." Computer Graphics Forum. Vol. 33. No. 4. 2014. Wrenninge, Magnus, Ryusuke Villemin, and Christophe Hery. Path traced subsurface scattering using anisotropic phase functions and non-exponential free flights. Tech. Rep. 17-07, Pixar. https://graphics. pixar. com/library/PathTracedSubsurface, 2017.